Soru 1: Geçici olay ve sürekli olay nedir?
⇒Geçici olay: Sistemlerin bir sürekli olaydan ikinci sürekli duruma geçerken gösterdikleri davranışlara geçici olay denir.
⇒Sürekli olay: Sistem içerisinde bulunan kondansatör ve endüktans gibi elemanların, sistemin ilk çalışmasından itibaren empedans değerlerinin sabit değere ulaştığı andan sonraki çalışma sürecine sürekli olay denir.
Soru 2: Kondansatör ve endüktans elemanlarına ait akım gerilim bağıntılarını belirleyiniz.
⇒Kondansatör
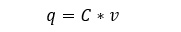
v: plakalar arasına uygulanan gerilim
C: kapasite değeri
Bu denklemden elde edilen tanım; kapasite, kondansatörün bir plakasındaki yükün iki plaka arasındaki potansiyel farka oranıdır(1 farad = 1 coulomb/volt).
Bir kondansatörün C kapasitesi, q yükünün uygulanan gerilime oranı olmasına rağmen, kapasite q ve v‘ye bağlı değildir. Kapasite, kondansatörün fiziksel boyutlarına bağlıdır.
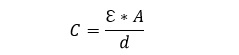
d: plakalar arası uzaklık
ℇ : plakalar arasındaki dielektrik malzemenin bağıl geçirgenliği
Bu denklem sadece paralel plakalı kondansatörlere uygulanmasına rağmen, genel olarak kapasitenin değerini belirleyen üç temel faktör vardır:
1. Plakaların yüzey alanı; daha büyük alan, daha büyük kapasite.
2. Plakalar arasındaki mesafe; daha küçük mesafe, daha büyük kapasite.
3. Malzemenin bağıl geçirgenliği; daha yüksek bağıl geçirgenlik, daha büyük kapasite.
Kondansatörün akım-gerilim ilişkisini elde etmek için, q=C*v denkleminin her iki tarafının türevini alırız.
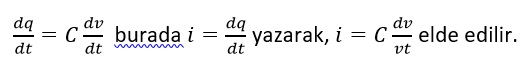
Kondansatörün gerilim-akım ilişkisi ise aşağıdaki gibi elde edilir.
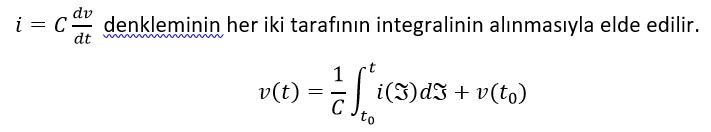
⇒Endüktans
Bir endüktanstan akım geçmesine izin verilirse, endüktansın uçlarındaki gerilim akımın değişiminin zamana oranı ile doğru orantılı olarak bulunur. Bu da bize endüktansın gerilim-akım ilişkisini verir.
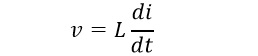
Endüktansın birimi henry (H)’dir. 1 henry = 1 volt-saniye/amper dir.
Endüktans, bobinin fiziksel boyutuna ve yapısına bağlıdır. Farklı şekillerdeki endüktans hesabı için gerekli formüller elektromanyetik teoriden elde edilir.
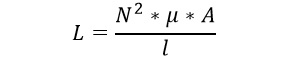
l: telin uzunluğu
A: telin kesit alanı
μ: çekirdeğin geçirgenliği
Bu denklemden bobinin sarım sayısının artırılması, çekirdek olarak daha yüksek geçirgenliğe sahip malzeme kullanılması, kesit alanının artırılması veya bobinin uzunluğunun azaltılmasıyla endüktansın artabileceğini görebiliriz.
Soru 3: Bir kondansatörün bir direnç üzerinden dolarken ve boşalırken uçlarındaki gerilimin zamana bağlı değişimine ait denklemleri grafikleriyle birlikte belirleyiniz.
⇒Kondansatörün Dolması
Aşağıdaki devre kondansatörün dolması ve boşalması sırasındaki gerilim değişiminin analizi için kullanılacaktır. Anahtar 1 konumundayken kondansatör E gerilim kaynağı tarafından R direncinin ve kondansatörün C sığasının belirleyeceği hızla dolar.
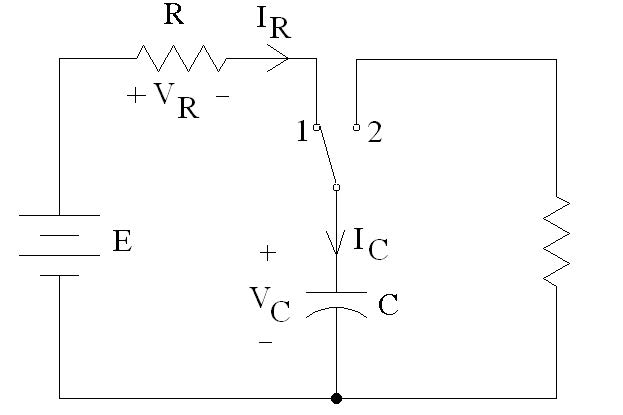
anahtarın 1 konumu için şu eşitlikler yazılabilir.

şeklindeki, kondansatör geriliminin zamanla değişimini gösteren ifadeye ulaşılır.

Yani başlangıçta boş olan ideal kapasitör, potansiyel fark sonucu akan akımla yavaş yavaş dolar ve belirli bir süre sonra kapasitör gerilimi E değerine ulaşacağından akım akmaz, kapasitör gerilimi bu değerde sabitlenir. R*C çarpımı devrenin “zaman sabiti” olarak adlandırılır.’τ‘ ile gösterilir ve birimi saniyedir. (1) ifadesinde t = τ için,
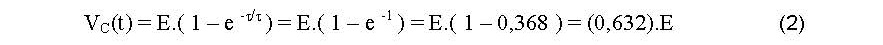
bulunur. Yani, kapasitör boşken devreye bağlanırsa τ saniye sonra kapasitör üzerindeki gerilim E değerinin 0.632 sine ulaşmış olacaktır. Yaklaşık 5τ saniye sonunda kapasitörün dolmuş olduğu söylenebilir.
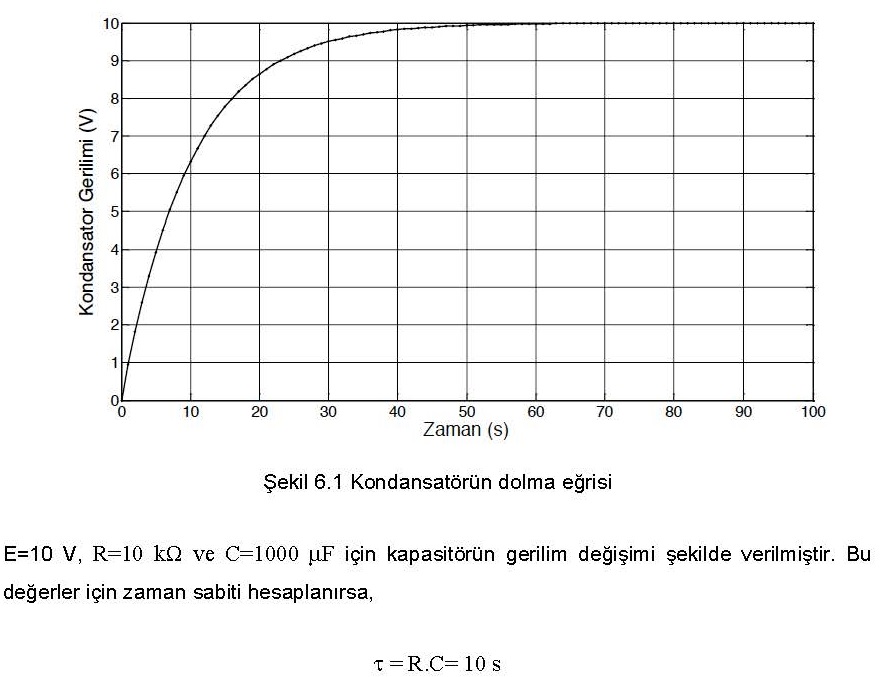
bulunur. Eğiriye dikkat edilirse 10 saniye sonra kapasitör gerilimi 6.32 V’a ulaşmıştır. 50 saniye sonra kapasitörün 10 V’a ulaştığı söylenebilir.
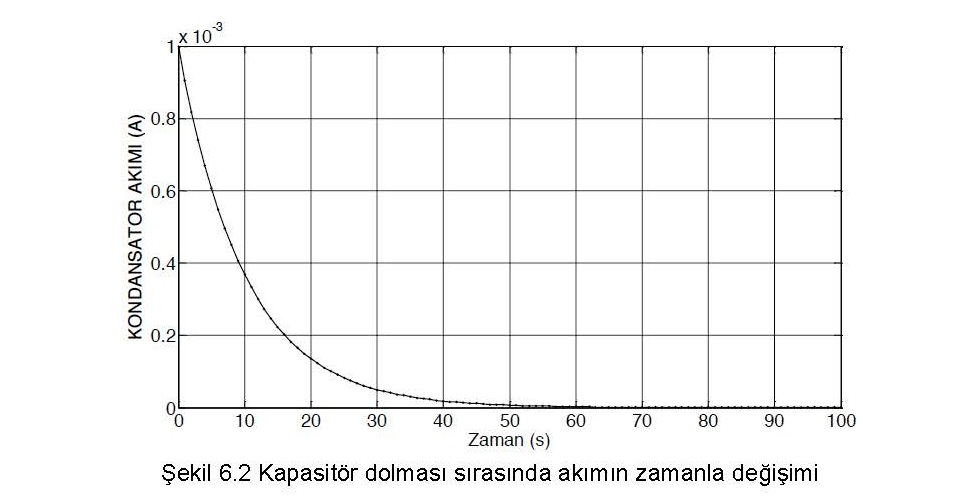
Kapasitörün gerilim değişimini bildiğimize göre akım değişimini de bulabiliriz. Kapasitör geriliminin üstel artması sonucu, bir ucu DC gerilim kaynağına diğer ucu kapasitöre bağlı bulunan r direncinin üzerindeki gerilim de üstel olarak azalır. Bu fark diren. üzerinden geçen akımı ve dolayısıyla seri bağlı olduklarından kapasitörü dolduran akımı oluşturur. Bu nedenle devreden geçen akım, R direnci uçlarındaki potansiyel farkın maksimum olduğu ilk andan en büyük değerini alacak kapasitörün dolmasıyla üstel olarak azalarak sıfıra doğru azalacaktır. Matematiksel olarak ise akan kapasitör geriliminin zamana göre türevinin C ile çarppımıdır. Dolayısıyla genel olarak,

olmaktadır. İlk başta kapasitör gerilimi sıfır olduğundan direnç doğrudan toprağa bağlıymış gibi düşünebiliriz. Daha sonra, artan kapasitör gerilimiyle akım azalır ve
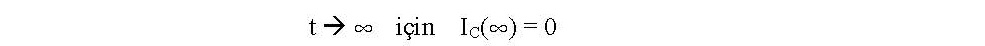
olur. Yani kapasitör dolduğunda artık içerisinden akım geçmez.
⇒Kondansatörün Boşalması
Şimdi, daha önce E gerilimine kadar dolmuş olan kapasitörü, anahtarı 2 konumuna alarak R direnci üzerinden boşaltalım. Daha önceki elektrik alan sonucu kapasitörün üst tarafında birikmiş olan yükler R direncinin kapasitör plakaları arasında köprü olmasıyla iki tarafta dengelenir ve kapasitör boşalmış olur.


Soru 4: İkinci dereceden sabit katsayılı homojen diferansiyel denklemlerin çözüm aşamalarını anlatınız.
⇒

Soru 5: E gerilimiyle dolu olan bir kondansatörün birbirine seri bağlı R ve L üzerinden boşalırken uçlarındaki gerilimin zamanla değişimini inceleyiniz.
Soru 6: Breadbord (Devre tahtası) özelliklerini inceleyiniz ve bir breadbord üzerinde elektrik devresinin nasıl kurulacağı hakkında bilgi veriniz.
⇒Altıncı sorunun cevabına buradaki paylaşımdan ulaşabilirsiniz.